|
|
Riemanns Habilitationsschrift
Von Jason Ross
Das Basement-Wissenschaftsteam hat auf der Internetseite des LaRouche-Aktionskomitees LPAC einen 40minütigen Film zur Einführung in Bernhard Riemanns Habilitationsschrift veröffentlicht ( http://www.larouchepac.com/node/18890). Es folgt der aus dem Englischen übersetzte Text.
Ein Verständnis des Inhalts von Bernhard Riemanns Habilitationsschrift ist entscheidend dafür, sämtliche wichtigen Bereiche des Denkens grundlegender zu begreifen und weiterzuentwickeln. Diese Schrift Riemanns, die häufig als mathematische Darstellung mißverstanden wird, ist Ausdruck seiner Sicht des physischen Universums und des menschlichen Geistes und gibt uns gleichzeitig nützliche Einblicke in gesellschaftliche Prozesse. In diesem Video gehen wir auf den Inhalt von Riemanns Schrift ein und erläutern einen wichtigen Umstand unseres Geisteslebens: Der Mensch sitzt nicht außerhalb des Universums und untersucht es von einem festen, stabilen Ort aus, sondern die schöpferische Geistesaktivität des Menschen ist selbst eine Kraft des Universums und muß von jedem, der eine einheitliche physikalische Sicht der Welt sucht, als solche betrachtet werden. Machen wir uns ans Werk.
Habilitationsschrift
Über die Hypothesen, welche der Geometrie zugrunde liegen
Sie haben wahrscheinlich gehört, daß die Summe der Winkel eines Dreiecks 180° oder zwei rechte Winkel ergibt. Sie haben auch gehört, daß sich zwei parallele Linien nie schneiden, selbst wenn man sie ins Unendliche verlängert. Das sind gewagte Behauptungen. Ein Dreieck auf einer Kugel hat drei rechte Winkel (Abb. 1), und diese scheinbar parallelen Linien schneiden sich, wenn man sie genügend verlängert.
Abb. 1: Die Euklidischen Gesetze sind abstrakte Konstruktionen, sie gelten nicht
im gekrümmten Raum - so hat dieses Dreieck auf einer Kugeloberfläche drei rechte
Winkel.
Was würde unser Geometrielehrer dazu sagen? Wahrscheinlich ist seine Antwort noch geläufig: „Diese Regeln funktionieren bestens, wenn die Linien gerade sind!“ Aber, so frage ich, was bedeutet es eigentlich, daß eine Linie gerade ist? Läßt sich dafür eine Definition angeben? Ist es vielleicht die kürzeste Entfernung zwischen zwei Punkten? Wenn das stimmt, dann sind die Linien auf unserer Kugel gerade. „Aber die Kugel ist gekrümmt“, könnte man einwenden, „ziehe die Linien bitte im Raum!“ Schön - aber wie soll das gehen? Vielleicht sollte man ein Lineal benutzen, doch woher will man wissen, daß ein Lineal gerade ist? Vielleicht sollte man einen Lichtstrahl, d.h. einen physikalischen Prozeß, benutzen. Aber das geht auch nicht, denn Licht wird gebeugt.
Wie man sieht, besteht das Problem darin, daß wir alle, ohne es zu merken, bestimmte Hypothesen über die Natur des Raumes und vorgefaßte Meinungen über Konstruktionen im Raum haben, etwa darüber, wie man parallele Linien erzeugt. Der berühmte Fälscher Euklid hatte gar nicht hinterfragt, ob seine Annahmen zutreffen; er schrieb seine Geometrie einfach so auf, daß sie mit diesen Annahmen (einschließlich der des ebenen Raums) übereinstimmte, ohne zu zeigen, daß sie überhaupt gültig wären! Und noch anmaßender als die einzelnen falschen Annahmen Euklids war, daß seine Axiome lediglich auf dem apriorischen Denken seiner Vorstellung statt auf realen, physikalischen Experimenten beruhten.
Bis zu Riemanns Zeit waren die Hypothesen über die Grundlagen von Raum und Geometrie nicht allgemein untersucht worden, ja man hatte nicht einmal erkannt, daß diese Grundlagen eigentlich nur Hypothesen waren. Um seine Überlegungen zu verdeutlichen, mußte Riemann eine allgemeine Vorstellung dessen entwickeln, was er die „Mannigfaltigkeiten“ einer Vielzahl von Dimensionen nannte, und die möglichen Krümmungen dieser Mannigfaltigkeiten aufzeigen. Dann konnte er zur Gestalt des tatsächlichen von uns bewohnten Raums zurückkehren und entscheiden, wie - und auf welcher Basis - sich dieser von anderen vorstellbaren Räumen unterscheidet. Das war etwas, was man nicht durch Logik lösen konnte; die Antwort ließ sich nur über den Weg ständiger Experimente finden.
Nehmen wir uns daher nun das Konzept der Mannigfaltigkeiten ganz allgemein vor.
Abschnitt I
Mannigfaltigkeiten im allgemeinen
Beginnen wir mit den Größen - was ist das eigentlich? Riemann sagt, eine Größe sei ein allgemeines Konzept mit vielfältigen speziellen Anwendungen oder Seinsmöglichkeiten oder Spezialisierungen. „Länge“ ist beispielsweise ein einheitliches Konzept mit vielfältigen Spezialisierungen wie etwa „zwei Zentimeter“, „drei Meilen“ oder „fünf Kilometer“. Das sind alles spezifische Längen. Geschmack ist ein weiteres Beispiel: „Salzig“, „süß“ oder „nach Oregano schmeckend“ sind spezifische Fälle des allgemeinen Konzepts „Geschmack“. Schuhgröße, Temperatur, Ort - alles sind Größen.
Dabei lassen sich zwei verschiedene Arten von Größen unterscheiden: solche, die sich durchgehend ändern, und solche, die sich in bestimmten Sprüngen ändern. Ein Beispiel: Die Töne, die man auf einem Cello spielen kann, sind stetig, die auf einem Klavier dagegen diskret. Auf dem Klavier gibt es zwischen H und C keine Taste, aber das Cello kann beide Töne variieren.
Eine weitere Überlegung ist, ob die genaue Angabe (oder „Bestimmungsweise“) einer Größe nur einen oder mehrere Werte erfordert. Ein Beispiel ist die Position auf der Erde. Längen lassen sich immer der Größe nach ordnen, man kann immer sagen, welche kürzer und welche länger ist, aber auf die Position trifft das nicht zu. Ein Ort hat immer eine Breite und eine Länge, und die Positionen lassen sich wohl nach der Länge oder nach der Breite anordnen, nicht aber nach ihrer Position. Die Position von New York ist weder größer noch kleiner als die Position von Houston. Größen oder „Mannigfaltigkeiten“, für deren Positionsbestimmung man zwei Angaben braucht, nennt man auch „zweifach ausgedehnt“. Um beispielsweise den Ort auf einer dieser unterschiedlichen Flächen zu bestimmen, braucht man zwei Werte - hier sieht man eine Kugel, eine Fläche, einen Affensattel und ein Katenoid (Kettenlinie).
Überdies läßt sich derselbe Ort auf derselben Fläche auf verschiedene Weise bestimmen. Man kann mehrere unterschiedliche Koordinatensysteme verwenden, um die Bewegung eines Punktes auf einer ebenen Fläche sichtbar zu machen. Die Koordinaten sind dabei gekrümmt, die Fläche jedoch nicht.
Geht man über die Fläche hinaus, so ist eine Position im Raum dreifach ausgedehnt. Man kann einen Ort im Raum auf verschiedene Weise festlegen, immer sind jedoch mindestens drei Angaben erforderlich. Man kann beispielsweise die Position XYZ für Breite, Länge und Höhe angeben, oder man kann zylindrische - oder auch katenoide - Koordinaten verwenden. Mit allen kann man auf unterschiedliche Weise einen Ort im Raum beschreiben, genauso wie man auf verschiedene Weise die Bewegung eines Punktes auf der Fläche sichtbar machen kann. Als Koordinatensysteme zeigen sie nicht an, daß der Raum gekrümmt ist.
Gehen wir eine Stufe weiter. Eine ebene Fläche und eine Kettenlinie haben ja nicht nur unterschiedliche Koordinatensysteme, sondern auch unterschiedliche Eigenschaften. Zum Beispiel paßt eine Fläche nicht auf ein Katenoid, man müßte sie biegen und dehnen. Können Sie sich einen anderen Raum vorstellen? D.h. können Sie sich einen dreidimensionalen Raum vorstellen, der nicht eben ist? Es ist schwierig, sich nicht einfach ein gekrümmtes Objekt im Raum vorzustellen, wenn man darüber nachdenkt. Wir kommen später auf diese Frage zurück, wenn wir mehr Munition zur Stärkung unserer Vorstellungskraft gekrümmter Räume beisammen haben.
Ein weiteres Beispiel: Wie viele Dimensionen hat die Farbe, die vom menschlichen Auge wahrgenommen wird? Wenn Ihnen bekannt ist, wie Farbe im Fernsehgerät oder dem Computerbildschirm dargestellt wird, wissen Sie, daß sämtliche Farben aus verschiedenen Mischungen von rotem, grünem und blauem Licht erzeugt werden und es damit dreidimensional ist. Farbe läßt sich auf viele weitere Arten darstellen, etwa nach dem YUV-Farbmodell, dem L*a*b*-Farbraum oder dem HSV-Raum nach Ton, Sättigung und Hellwert (im Bild), aber sie sind alle dreidimensional.
Die dreifache Ausdehnung ist aber keine Eigenschaft des Lichtes, sondern eine Eigenschaft des menschlichen Auges, das drei unterschiedliche Farbrezeptoren besitzt. Das kann einen täuschen, denn wenn man rotes und gelbes Licht mischt, erscheint es uns orange, aber es wird dadurch keine oranges Licht - Rot und Gelb läßt sich durch ein Prisma wieder voneinander trennen. Eine andere Macke des Sehens ist z.B., daß die Farbe Magenta im Farbspektrum gar nicht zwischen Rot und Violett liegt, das ist nur, wie unser Geist die Erfahrung der Sinne zusammenbringt. Während für uns Farbe dreidimensional ist, ist sie für Vögel, die vier verschiedene Farbrezeptorzellen haben, vierdimensional!
Das führt uns zum Beispiel einer Größe, die so viele Dimensionen hat, daß man sie gar nicht mehr zählen kann. Dieses Beispiel ist das Licht selbst, das eine unendliche Zahl von Spezifikationen hat, um es genau zu beschreiben. Das taucht beim Farbabgleich auf, wo die drei Farbdimensionen auf einem Bildschirm einfach nicht mehr ausreichen - unter bestimmten Lichtverhältnissen mag die Farbe stimmen, bei anderen aber nicht. Man kann sehen, wie der Abgleich je nach Lichtart besser oder schlechter ist.
Hier ist die Farbkurve für eine bestimmte Farbe des professionellen Lichtfilters - für jede mögliche Farbe im Spektrum überträgt der Filter einen bestimmten Lichtanteil -, so daß jede der unendlichen Zahl von Farben im Regenbogen einen eigenen Durchlaßwert hat: Das tatsächliche Licht (im Gegensatz zum wahrgenommenen Licht) hat nicht drei, sondern unendlich viele Dimensionen! Hier sieht man die wahrgenommene Farbe einer veränderlichen Farbkurve. Es gibt im Licht ungeheuer viel, was unser Auge gar nicht unterscheiden kann!
Mit diesen allgemeinen Konzepten von Größen gewappnet, können wir nun zu Riemann zurückkehren, um zu untersuchen, welche unterschiedlichen Maßverhältnisse auf Mannigfaltigkeiten zutreffen, und wie man sie bestimmen kann. Was unterscheidet eine Kugel von einer Fläche?
Abschnitt II
Mögliche Maßverhältnisse
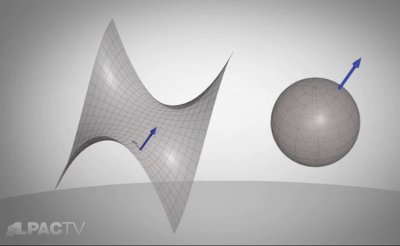Abb. 2: Um die Eigenschaften gekrümmter Oberflächen beschreiben zu
können, verwendete Carl Friedrich Gauß die Ausrichtung der Normale
(Senkrechten), die er, auf einer Kugel dargestellt, wie eine Kompaßnadel
verwendete.
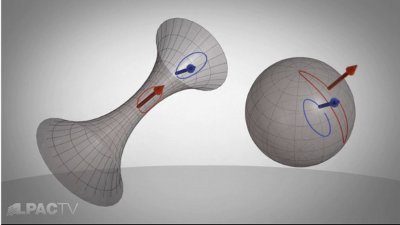Abb. 3: Scheinbar gleiche Bewegungen auf gekrümmten Oberflächen
erzeugen, wenn man sie mithilfe der Normalen auf eine Kugeloberfläche überträgt,
z.T. sehr ungleiche Flächen.
Um unsere Untersuchung der inneren Eigenschaften von Mannigfaltigkeiten zu beginnen, fangen wir mit zweidimensionalen gekrümmten Flächen an, und hierbei benutzen wir den Ansatz des großen Wissenschaftlers Carl Friedrich Gauß, der Riemann das Thema für seine Vorlesung vorschlug und diese mit Freude verfolgte. Gauß hatte eine ganz allgemeine Methode entwickelt, um mit spezifischen Techniken gekrümmte Flächen zu untersuchen.
Zum Beispiel ist die Kugel gekrümmt und die Fläche ist eben. Hier ist eine andere Form, die man Affensattel nennt. Im Gegensatz zur Fläche ist sie gekrümmt, aber nicht genauso wie die Kugel. Läßt sich seine Krümmung quantifizieren? Als erste Technik hierfür führen wir die Normale ein - eine Richtung an jedem Punkt der Fläche, die senkrecht direkt von ihr wegzeigt. Man benutzt die Normalen einer Fläche, um deren Krümmung zu messen.
Hierbei bildete Gauß die Normalen auf einer Hilfskugel ab, wobei er nur die Richtung der Normalen, nicht aber ihren Ort beibehielt. (Abb. 2) Man kann sich den Affensattel auch als unglaublich klein und im Mittelpunkt eines Kreises vorstellen, so wie wir auf der Erde auf entfernte Sterne zeigen. Betrachten wir die Richtung der Normalen, wenn wir uns auf der Fläche bewegen. Wenn wir uns auf der Fläche nach rechts bewegen, bewegt sich die Richtung, auf die die Normale zeigt, manchmal nach links. Die Kugel dient uns dabei als eine Art dreidimensionaler Kompaß, um räumliche Richtungen anzeigen zu können, ähnlich wie wir am Rand eines gewöhnlichen Kompasses die Richtung auf der zweidimensionalen Erdoberfläche ablesen.
Gauß’ erster Ansatz zur Messung einer gekrümmten Fläche war, eine Region auf der Fläche zu wählen und sie mit der Größe der entsprechenden Fläche auf der Hilfskugel zu vergleichen. Je größer die Fläche auf der Kugel, desto gekrümmter die Region auf der Fläche. Hier ist die rote Region um das mehrfache gekrümmter als die blaue Region. (Abb. 3)
Um die Krümmung an einem bestimmten Punkt zu messen, verkleinerte er die Region so lange, bis sie verschwindend klein war. Mit Hilfe dieser Technik stellen wir fest, daß ein Zylinder überhaupt keine Krümmung hat - er ist nach Gauß’ Methode flach! Überstreicht man diese vierseitige Region auf dem Zylinder, ist die von den Normalen gebildete Region lediglich eine gerade Linie ohne Flächeninhalt: Null Krümmung.
Bei seiner nächsten Technik zur Messung von Krümmungen benutzte Gauß sogenannte oskulierende [= (sich) berührende] Kreise. Genauso wie zwei beliebige Punkte eine Richtung anzeigen, wenn man sie miteinander verbindet und eine Linie durch sie zieht, bilden drei beliebige Punkte einen Kreis. Legt man also eine Ebene durch eine Fläche, ergibt sich eine Kurve, und es gibt immer einen Kreis, der an diesem Punkt am besten zu dieser Kurve paßt. Hier sieht man die Reihe oskulierender Kreise für einen bestimmten Punkt auf der Fläche.
Gauß zeigte, daß die extremsten oskulierenden Kreise stets an Flächen auftreten, die senkrecht zueinander stehen; wenn man dann die Radien der beiden Kreise multipliziert und den Kehrwert nimmt, erhält man das gleiche Krümmungsmaß, das sich zuvor mit den Normalen ergab. Wieder stellen wir fest, daß ein Zylinder keine Krümmung hat: Ein extremer oskulierender Kreis ist der Radius des Zylinders, während der andere als gerade Linie mit unendlichem Radius erscheint. Eins geteilt durch das Produkt der beiden Radien ist null.
Bevor wir zu Gauß’ dritter Methode kommen, die für Riemann am wichtigsten war, wollen wir ein besonderes historisches Beispiel aufgreifen: die Berechnung des Erdumfangs. Soweit wir wissen, geht diese Entdeckung auf den einstmaligen Bibliothekar von Alexandria, Eratosthenes von Cyrene, im 3. Jahrhundert v.Chr. zurück. Er hatte bemerkt, daß die Sonne am Tag der Sommersonnenwende in Assuan direkt im Zenit stand. Dann vermaß er am gleichen Tag des Jahres die Schatten in Alexandria. Unter der Annahme, daß die Sonne so weit entfernt war, daß man ihre Strahlen als parallel ansehen konnte, und aus der Kombination des Winkels der Schatten und der Entfernung der beiden Städte berechnete er den gesamten Erdumfang auf 250.000 Stadien (39.625 km), was eine bemerkenswert genaue Angabe war. So wurde eine Eigenschaft des gesamten Planeten bestimmt, indem man Messungen in einem kleinen Bereich vornahm.
Abb. 4: Für „zweidimensionale“ Wesen erschiene die Oberfläche einer sehr
goßen Kugel wie eine ebene Fläche...
Abb. 5 a-d: ... aber die Krümmung einer Oberfläche hat doch Wirkungen, die
sich auch innerhalb eines zweidimensionalen Raums feststellen lassen - etwa
durch die Änderung von Richtungen: Bewegt man den Pfeil auf einer Kurve entlang
der Seiten eines Dreiecks, so hat er eine andere Richtung, wenn man wieder zum
Ursprungsort zurückkehrt.
Nun sind wir darauf vorbereitet, zwei verschiedene Kategorien von Flächeneigenschaften zu unterscheiden: äußere (extrinsische) Eigenschaften und innere (intrinsische) Eigenschaften. Alle bisher angeführten Beispiele betrafen äußere Eigenschaften, die sich auf äußere Objekte und Positionen beziehen. Um demgegenüber innere Eigenschaften anzuführen, kann man folgendes fragen: Wie hätte Eratosthenes den Erdumfang berechnen können, wenn unsere Atmosphäre ständig wolkenverhangen wäre, wie etwa auf der Venus? Welche Technik würde ihm zur Verfügung stehen, um bestimmte Merkmale der Erde zu entdecken, wenn er sich nur auf die Erdoberfläche hätte stützen und keine Sonne ihm von außen hätte helfen können?
Um es noch ein wenig schwerer zu machen, nehmen wir an, daß wir selbst nur zweidimensionale und keine dreidimensionalen Wesen wären. Ein bekanntes Beispiel hierfür findet sich in dem Buch Flatland (Flächenland) von E.A. Abbot, worin der Autor über eine Welt schreibt, in der es nur zwei Dimensionen gibt. Die Bewohner sind Striche, Dreiecke, Vierecke und andere Vielecke, wobei die Anführer viele Seiten mit annähernder Kreisform haben. Was nun, wenn da etwas nicht stimmt? Wenn das Flächenland in Wirklichkeit ein „Kugelland“ wäre?
Die einzelnen Bewohner bzw. Gebilde würden, wenn sie sich auf einer riesigen Kugel bewegen, zwar von einem Ort zum anderen keinen Unterschied feststellen, könnten aber dennoch Anzeichen dafür bemerken, daß irgend etwas nicht ganz flach ist. Zwei derartige Hinweise gäben ihnen der Satz des Pythagoras sowie Richtungsänderungen.
Beim Satz des Pythagoras geht es um drei Quadrate, deren Anordnung ein rechtwinkliges Dreieck ergibt. Jeder hat in der Schule gelernt, daß A2 plus B2 gleich C2 ergibt. Aber wie kann man wissen, daß dies wirklich stimmt? Bilden wir einfach zwei größere Quadrate, indem wir einige gleiche Dreiecke hinzufügen. Diese beiden größeren Quadrate haben die gleiche Größe und Fläche. Entfernt man von beiden vier gleiche Dreiecke, sollte der Rest ebenfalls gleich sein - also sind A2 und B2 tatsächlich genauso groß wie C2.
Wie wir jedoch bereits oben gesehen haben, ist das auf einer Kugelfläche ganz anders. Wir erinnern uns an unser Dreieck mit drei rechten Winkeln. Welche Seite ist hier A, welche B und welche C? Der Satz des Pythagoras ist hier sicherlich nicht gültig. Er muß in einer Weise modifiziert werden, daß sich daraus eine Lösung für die Flächenland-Vielecke ergibt - eine Technik, um die Form ihrer Welt von innen zu entdecken. Aber erinnern wir uns, wie wir uns gekrümmten Raum vorzustellen versuchten - wie könnten die [die „Flächenland“-Bewohner] sich dort eine gekrümmte Fläche vorstellen? Die Anomalien sagen ihnen, was los ist, auch wenn sie sich eine Kugel bildlich nicht vorstellen können, weil die dreidimensional ist, sie aber zweidimensional sind.
Bei einer zweiten Technik geht es um die Richtung. Man kann durch eine Stadt oder ein Gebäude laufen und sich dabei merken, wo Norden ist, indem man eine Übersicht über alle Abbiegungen behält, die man gemacht hat. Hier ist ein Beispiel auf einer Fläche.
Und das gleiche wollen wir auf einer Kugel tun. Wir bewegen uns auf der Kugel, während der Zeiger bei jeder Wendung in der gleichen Richtung bleibt. Doch wenn wir an den Ausgangspunkt zurückkehren, weist der Zeiger nicht mehr in die ursprüngliche Richtung. Bei einem erneuten Durchlauf ändert sich die Richtung erneut, obwohl der Zeiger während des Verlaufs nicht verdreht wurde.
Beide Techniken, der Satz des Pythagoras und die Richtungsbewegung, sind innere Eigenschaften der Fläche, sie haben keinen Bezug zu etwas außerhalb der Fläche, noch nicht einmal zu der Vorstellung eines außerhalb gelegenen Raums. Zusammengefaßt: Alles, was die Vieleck-Wesen tun oder lernen können, bezieht sich auf das Innere, ist intrinsisch.
Gauß macht dann zwei erstaunliche Aussagen. Die eine ist, daß sich keine der inneren Eigenschaften ändert, wenn die Fläche gebogen wird, solange man sie nicht streckt. Das heißt, biegt man eine Fläche zu einem Zylinder und wieder zurück, ändert sich an der Oberfläche gar nichts; die Entfernungen zwischen den Punkten, die kürzeste Linie zwischen zwei Punkten, den Winkeln usw. alles bleibt unverändert. Die „Flachlandbewohner“ würden keinerlei Unterschied bemerken. Ähnlich haben das Katenoid und das Helikoid die gleichen inneren Eigenschaften und entstehen, indem man das eine in das andere umfaltet.
Gauß’ zweiter Durchbruch bestand darin, daß er einen Weg fand, die Krümmung an jedem Punkt intrinsisch zu messen, so wie es die ebenen Vieleck-Wesen vermochten, was bedeutete, daß die Fläche eine eigene abgeschlossene Welt bilden konnte und es unnötig ist, ihr eine bestimmte Gestalt im Raum zu geben (wie etwa Zylinder contra Fläche). Man braucht dazu keine Normalen oder oskulierenden Kreise. Die Oberfläche läßt sich von innen verstehen.
Diese Erkenntnis war entscheidend für Riemanns Untersuchung gekrümmter Räume. Dreifach ausgedehnte Mannigfaltigkeiten (wie der Raum) können gekrümmt sein! Hierbei kann man aber nur an intrinsische Krümmung denken, da wir nicht von einer vierten Dimension aus dem Raum heraustreten können, um auf ihn herabzusehen, so wie man auf zweifach ausgedehnte Flächen herabschauen kann. Vielmehr stecken wir in den gleichen Schuhen wie unsere Vieleck-Freunde, wenn wir die Form des Raumes um uns herum bestimmen wollen. Riemann schildert in seinem Papier die allgemeinst mögliche Weise, um die Krümmung innerhalb einer Mannigfaltigkeit zu bestimmen. Die anomalen Eigenschaften von Wirkung und Bewegung definieren die Krümmung.
Was ist nun, ausgehend von allen diesen Möglichkeiten, die Form des tatsächlichen Raums, im Gegensatz zu irgendwelchen mathematischen Tagträumen?
Abschnitt III
Gekrümmte Räume verstehen
Wenn wir diese Überlegungen auf die tatsächliche Gestalt des physikalischen Raums anwenden, sollten wir zunächst die beiden unterschiedlichen Konzepte von Unbegrenztheit und Unendlichkeit gegenüberstellen, welche oft miteinander verwechselt werden. Nehmen wir eine Kugel als Beispiel: Bewegung auf der Kugel stößt auf keine Grenzen, hat also keine Begrenzungen; dennoch ist die Kugel nicht unendlich, sie hat eine meßbare Gesamtgröße, während Bewegung unbegrenzt ist. Der Raum selbst scheint zwar in jeder Hinsicht unbegrenzt zu sein, doch kann man daraus nicht schließen, daß er unendlich ist. Der Raum könnte endlich sein.
Noch eine andere Überlegung: Fragen wir uns, ob Gegenstände von der Position unabhängig sind. Nehmen wir als Beispiel den Unterschied zwischen einer Orange und einer Wassermelone oder einer anderen Frucht. Auf einer Orange läßt sich die Schale ohne Dehnung von einem Ort zum anderen verschieben; es gibt keinerlei Unterschiede, alle Teile sind gleich. Bei unserem anderen Beispiel ist das aber nicht der Fall. Die beinahe ebene Region hat eine bestimmte Beziehung zwischen Umfang und Fläche, aber dort hat der gleiche Umfang eine größere Fläche! Die Bewegung von einem Ort zum anderen erfordert eine gewisse Dehnung. In drei Dimensionen wäre dies wie die Bewegung einer Orange im Raum, wobei das Innere größer gedehnt wird, obwohl die äußere Schale die gleiche Größe behält.
So etwas will man wahrscheinlich vermeiden. Dazu könnten wir zunächst von der Hypothese ausgehen, daß Gegenstände von der Position unabhängig sind, was bedeutete, daß jeder Teil des Raumes die gleiche Krümmung wie jeder andere hätte. Wäre dieses Maß auch nur geringfügig positiv, wäre der Raum endlich. Das würde sich in der Astronomie zeigen, wo derselbe Stern aufgrund der Krümmung des dazwischen liegenden Raums in zwei entgegengesetzten Richtungen erscheinen könnte. Man kommt immer wieder zum Ausgangspunkt zurück, in welche Richtung man auch aufbricht. Selbst wenn man nicht ganz herum kommt, könnte derselbe Stern auf den unterschiedlichsten Bahnen erscheinen, d.h. er sähe nicht wie ein Punkt, sondern wie ein Ring oder Heiligenschein aus.
Doch in der Astronomie sehen wir keine verdoppelten Sterne oder „Heiligenschein“-Sterne, selbst wenn wir in sehr große Fernen blicken. Wenn also der Raum gleichförmig wäre, müßte er eben oder nahezu eben sein. Was aber, wenn der Raum nicht gleichförmig ist? Wenn Gegenstände nicht positionsunabhängig sind? Was wäre, wenn sich die räumlichen Beziehungen von Ort zu Ort änderten? Dann könnten wir von dem, was wir aus dem Großen in der Astronomie entdeckt haben, nicht auf die Beziehungen im Kleinen rückschließen.
Tatsächlich gab es zu Riemanns Zeiten Durchbrüche in der Chemie und im Elektromagnetismus, dank neuer Hypothesen über die Natur von Vorgängen im sehr Kleinen. Die Maßverhältnisse im Kleinen konnten die verschiedensten Eigenschaften aufweisen, solange die Krümmung auf sehr großem Maßstab wieder auf die aus der Astronomie abgeleitete annähernde Null-Krümmung hinauslief. Die vermeintliche Ebenheit oder Flachheit der Geometrie auf astronomischem Maßstab, wie man sie zu Riemanns Zeiten verstand, erweist sich auf der Mikroebene als nicht wahr.
Wie kann man nun die Maßverhältnisse im Kleinen herausfinden? Wie ist der Raum gekrümmt und, noch wichtiger, wie kann man entdecken, warum er so gekrümmt ist?
(Riemann:) „Bei einer diskreten Mannigfaltigkeit ist das Prinzip der Maßverhältnisse schon in dem Begriff dieser Mannigfaltigkeit enthalten, bei einer stetigen aber muß sie anders woher hinzukommen.“
Um das zu verdeutlichen: Beschreibt man oder denkt man sich eine diskrete Mannigfaltigkeit wie „die Tasten auf einem Klavier“ oder „die Menschen in einem Raum“, so hat man mit dem Begriff der Mannigfaltigkeit die Maßeinheit bereits vorgegeben. Bei einer stetigen Mannigfaltigkeit wie Länge oder Position hat man jedoch keine Vorstellung davon, wie der Raum aussieht oder wie man Messungen vornehmen sollte.
Riemann fährt fort: „Es muß also entweder das dem Raume zu Grunde liegende Wirkliche eine diskrete Mannigfaltigkeit bilden, oder der Grund der Maßverhältnisse außerhalb, in darauf wirkenden bindenden Kräften, gesucht werden.“ Genauso ist es! Die ganze Grundlage, der hinreichende Grund dafür, daß etwas so und nicht anders ist, liegt nicht darin, viele Beobachtungen davon zu machen.
Man hat den Eindruck, daß Riemanns Untersuchung nicht mit einem abschließenden Ergebnis endet. Tatsächlich stößt man am Ende von Riemanns Vorlesung an die Grenzen des mathematischen Theoretisierens im Elfenbeinturm. Seine Untersuchung kann zwar ungerechtfertigte Annahmen beseitigen, aber keine positive Aussage treffen. Riemann erklärt am Schluß: „Es führt dies hinüber in das Gebiet einer andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur der heutigen Veranlassung nicht zu betreten erlaubt.“
Damit wollen wir die Mathematik hinter uns lassen und uns in den Bereich der Physik, das Gebiet der Realität begeben.
„Das Gebiet der Physik“
Jenseits der Mathematik
Denken wir an Johannes Kepler und die Geburt der Astrophysik. Kepler betrat einen Bereich, in dem man bis dahin Forschung explizit vom Standpunkt einer Wahrnehmung der Natur mit den Sinnen betrieben hatte. Seine Vorgänger hatten verschiedene Modelle des Planetensystems vorgelegt, die alle „den Anschein wahren“ sollten - d.h. die Modelle sollten bei den Sinnen den gleichen Eindruck hinterlassen wie die Planeten auch. Kepler wies nach, daß die Modelle, selbst wenn sie so präzise wie möglich den Augenschein nachbilden sollten, aufgrund dieser Methode immer falsch waren. Außerdem wußte er, daß selbst eine falsche Hypothese manchmal wie die Wahrheit aussehen konnte. Er schrieb über seine eigene „Stellvertreterhypothese“:
„Sodann ist das, was einerseits die wahre, bisher noch unbekannte Hypothese, andererseits die falsche, von uns angenommene leistet, deswegen noch nicht gleich, weil beide merklich das gleiche zu leisten scheinen. Es kann ja immer noch ein ganz kleiner Fehler vorliegen, der sich den Sinnen entzieht.“
Es wird immer Dinge geben, die wir noch nicht gemessen haben. Selbst wenn unser Modell vollkommen mit den Beobachtungen übereinstimmt, heißt das nicht, daß es wahr ist - nicht nur, weil die Beobachtungen in der Zukunft besser werden, sondern weil übereinstimmende Beobachtungen zwar notwendig, aber nie allein der Maßstab für Wahrheit sind. Auch Kepler entwickelte ein funktionierendes mathematisches Modell für die Planeten, aber er gab sich nicht zufrieden, solange er keine Hypothese für den eigentlichen Beweggrund, den Zweck hinter diesen Bewegungen hatte. Warum bewegen sie sich so, wie sie sich bewegen? In seiner Neuen Astronomie äußerte er die Vermutung, daß eine Kraft in der Sonne die Bewegungen bewirkte. In seiner Weltharmonik beschrieb er im einzelnen die harmonischen Kompositionsprinzipien, die die spezifischen Bahnen, wie sie die Planeten anzeigten, erforderlich machten. In diesem Fall ist die Ursache der Zweck - es geht um das Warum und nicht um das Was oder Wie? Newtons verallgemeinertes Quadratabstandsgesetz mag angeben, wie sich die Bewegung von Augenblick zu Augenblick verändert, aber nicht warum - was Newton selbst zugab. Kepler bewies das Versagen der Mathematik und war als Wissenschaftler erfolgreich! Seine wunderbar einfache Frage „Warum so und nicht anders?“ erhob ihn über induktive Generalisierungen einer auf Sinneseindrücken beruhenden Welt und ließ ihn die Vorstellung einer Welt schaffen, die auf Prinzipien der Schönheit aufbaut und damit so streng wie frei ist.
Pierre de Fermat etablierte den Zweck als wissenschaftliches Konzept. Die Beugung des Lichts beim Übergang von einem Medium ins andere beschäftigte die Denker bereits seit Jahrhunderten - warum wird Licht gebeugt, wenn es beispielsweise in Wasser eintritt? Unter allen Wegen, die das Licht von seinem Ursprung zu seinem Ziel nehmen könnte, folgt es jenem Weg, der seine Reise am schnellsten macht. Hierbei hat die kürzeste Zeit nichts mit Sinneswahrnehmung zu tun. Sie hat die Eigenschaft eines Motivs, nicht einer Erscheinung.
Gottfried Wilhelm Leibniz zeigte, daß eine a-priori-Annahme von unabhängigem Raum und unabhängiger Zeit immer zu Absurditäten führt. Als der Newton-Vertraute Samuel Clarke zu beweisen versuchte, Gottes Allmacht läge in Gottes freier Wahl bei der Entscheidung, wo im Augenblick der Schöpfung alles entstehen sollte, antwortete Leibniz, dies sei überhaupt keine Entscheidung. Das Universum einen Meter nacht rechts zu verschieben, sei das gleiche, als wenn man den Raum einen Meter links bewegte. Die Beziehung zwischen den Gegenständen würde sich überhaupt nicht verändern, niemand würde es bemerken. Es ist völlig bedeutungslos. Die Absurdität entsteht aus der Annahme eines Raums, der vermeintlich vor und unabhängig von den Dingen existiert, die im Raum miteinander in Beziehung stehen. Es gibt keinen absoluten Raum.
Das sieht man auch, wenn man Descartes’ Bewegungsgesetze mit denen von Leibniz vergleicht. Descartes’ größtes Problem (jedenfalls eines seiner großen Probleme) ist, daß er an eine absolute Bewegung und absolute Ruhe glaubt, was ihn zu völlig verrückten Schlußfolgerungen treibt. Leibniz wußte, daß Bewegungen nur relativ sind, auch wenn die Ursache dieser Bewegungen real und absolut sein kann. Die Physik muß die Grundlage der Geometrie bilden, und davon ausgehend entwickelte Leibniz die Infinitesimalrechnung.
Denken wir an Albert Einstein. Seine Relativitätstheorie verwirft die voneinander getrennten geometrischen Vorstellungen von Zeit und Raum, statt dessen wird der physische Prozeß der Ausbreitung des Lichtes verwendet, um der Raum-Zeit eine physische Bedeutung zu geben; und indem er dies tat, zeigte er auf, wie sich die Raum-Zeiten für verschiedene Beobachter voneinander unterscheiden. Sie existieren als Wirkungsräume, aber nicht als geometrische Räume. Die physikalische Wirkung ist primär, und es werden Geometrien erzeugt, worin sich unsere Hypothesen über die wahren Beziehungen zwischen den sich entfaltenden Wirkungen im Universum widerspiegeln. Man muß die Geometrien so gestalten, daß sie der Physik entsprechen, und nicht andersherum. Heute wird Einsteins Allgemeine Relativitätstheorie (wenn auch nicht immer korrekt) als häufigstes Beispiel für eine gekrümmte Raumzeit angeführt.
Gehen wir nun über zur Biologie und darüber hinaus. Wladimir Wernadskij suchte leidenschaftlich nach einem Verständnis der Natur des Lebens und der Erkenntnis, und dazu suchte er nach Geometrien, mit denen sich Aktivitäten des Lebens beschreiben lassen, von denen er wußte, daß sie in einem Euklidischen Raum nicht existieren können. Ein Beispiel hierfür ist die Chiralität, die „Händigkeit“ lebender Prozesse. Pasteur und Curie hatten gezeigt, daß lebende Prozesse im Unterschied zu abiotischen Prozessen zwischen links- und rechtshändigen Versionen des gleichen Moleküls unterscheiden und eine dieser Versionen bevorzugen, was in einer einfachen Euklidischen Geometrie unmöglich wäre.
Wernadskij schrieb auch viel über verschiedene Formen der lebenden Zeit, die sich von der abiotischen Zeit unterscheiden. In der lebenden Zeit der Evolution beispielsweise unterscheiden sich vorher und nachher nicht bloß chronologisch, in dem Sinne, daß „vorher“ bloß „nicht nachher“ bedeutet und „nachher“ das Gegenteil von „vorher“. Vielmehr ist nachher fundamental anders als vorher, nämlich eine Zeit, in der höher entwickelte Lebensformen existieren.
Das sieht man noch stärker in der menschlichen Zeit. In unserer wirtschaftlichen Zeit ändert sich die Kraft der menschlichen Gattung - und wir sind selbst eine physische Kraft - mit jeder neuen Entdeckung eines Prinzips kategorisch. In der Wirtschaft unterscheiden sich die Zeiten qualitativ, nicht quantitativ. Und solche menschliche Zeit „läuft“ nicht einfach wie das Ticken einer Uhr, sondern sie muß durch Entdeckungen geschaffen und mit Leidenschaft vorangetrieben werden! Das ist die Raum-Zeit der wirtschaftlichen Entwicklung.
Euklid lag also nicht bloß mit bestimmten Axiomen falsch. Auch jede andere Geometrie, die von geometrischen Axiomen ausgeht statt von den Prinzipien, die reale physische Wirkungen bestimmen, würde ebenso irren. Mit Riemann ändert der Begriff „Geometrie“ an sich vollständig seine Bedeutung - sie ist keine Bühne mehr, auf der sich die Ereignisse entfalten, sie ist die Form der Wirkung selbst!
Was können wir über den Prozeß sagen, durch den wir etwas über diese Form erfahren? Ist unser Ziel ein endgültiges Verständnis der Natur, die wir beobachten, über die wir Hypothesen entwickeln und der wir uns asymptotisch annähern, ohne jemals dieses höchste Wissen zu erreichen? Nein: Wir selbst sind ein Teil dessen, was wir studieren!
Denken wir an die mächtigste aller physischen Kräfte: den menschlichen Geist. Das kreative Denken ist eine physische Kraft, es hat ebenso physische Wirkungen wie der Elektromagnetismus, Plasmen oder biologische Prozesse. Eine wahrhaft Riemannische Geometrie, die sich fest auf die Prinzipien gründet, die den wahrgenommenen Erscheinungen zugrunde liegen, muß den kreativen Geist berücksichtigen. Unser Ziel ist nicht, eine endgültige Geometrie der Welt da draußen zu finden: Diese muß vielmehr die sich entwickelnde Macht der Vernunft, den Kern der wirtschaftlichen Entwicklung, mit umfassen. Es darf keine Trennung geben zwischen dem Studium der Physik und dem Studium des Geistes. Naturwissenschaften, die den Geist ausklammern, können keine wahren Prinzipien finden, sie werden immer im Sumpf statistischer Induktion und Korrelation auf der Grundlage unserer Sinne steckenbleiben. Ebenso wird auch eine Sozialphilosophie oder Soziologie, die nicht vom Studium des fruchtbaren kreativen Denkens geprägt ist, bloß ein Studium von Neurosen oder langweiliger Belanglosigkeiten ohne jede nützliche Richtung sein.
Es gibt nur eine Welt, die wir entdecken und auf die wir einwirken können. Der Geist entdeckt, der Geist handelt, der Geist schöpft. Riemann führt uns in diese Realität und zeigt uns, daß die Prinzipien, die der Realität zugrunde liegen, mit dem Geist übereinstimmen. Er endete seine Vorlesung damit, daß man die Mathematik zugunsten der Physik aufgeben muß, doch wir müssen, um ein wahrhaft Riemannisches Programm zu verwirklichen, über die Physik zur Ökonomie hinausgehen - wir müssen die voranschreitende Entwicklung der Kräfte des menschlichen Geistes einschließen. Darin liegt Riemanns große Bedeutung für die Wirtschaftswissenschaft.