|
|

Die wahre Revolution: Wiedergeburt einer schönen Kultur
Jonathan Thron berichtet von einem Seminar der Bürgerrechtsbewegung Solidarität vom 19.-21. April in Dresden.
Richtig zu denken ist wichtiger, als das Richtige zu denken! Denn Fakten sind vergänglich und reproduzierbar, aber die notwendigen Fakten oder Technologien kann man nur mit der richtigen Denkmethode erzeugen. Zum Beispiel ist es zwar wahr, daß James Watt als erster die Dampfmaschine auf den Markt gebracht hat. Aber es war nicht seine Erfindung! Die Erfindung der Dampfmaschine wurde durch die Entdeckungen von Gottfried Leibniz möglich gemacht und die erste Dampfmaschine wurde bereits um 1700, etwa 70 Jahre vor Watts Maschine, von Denis Papin gebaut.1
Die Menschheitsgeschichte im richtigen Kontext zu sehen, ist unerläßlich. Aber fast noch wichtiger ist es, die Methoden zu erlernen, mit denen neue und notwendige Erfindungen und Entdeckungen gemacht werden können! Dafür ist eine Kultur der Wahrheitsfindung und des Strebens nach charakterlicher Schönheit notwendig.
Denn wie konnte eine so große Zivilisation wie die der alten Griechen untergehen? Die Schuld daran trug der Sophismus, die Abkehr vom Streben nach Wahrheit und Streben nach einer edlen Gesinnung. Diese Warnung sollten wir uns sehr zu Herzen nehmen, da die heutige Kultur – vor allem die westliche – genau das gleiche Problem hat.
Damit unsere heutige Welt nicht das gleiche Schicksal ereilt wie das untergegangener Zivilisationen, hat es sich die LaRouche-Bewegung zur Aufgabe gesetzt, die Freude am Entdecken der richtigen Denkmethode – wissenschaftlich wie auch kulturell – wieder in möglichst vielen Menschen zu entfachen. Unter genau diesem Motto stand ein Seminar der Bürgerrechtsbewegung Solidarität, das vom 19.-21. April 2019 in Dresden stattfand. Der Inhalt des Seminars waren vier Vorträge, einige Workshops und ein Musikabend – alles unter aktiver Beteiligung der Anwesenden.
 Abb. 1: Peter Møller bei seinem Vortrag.
Abb. 1: Peter Møller bei seinem Vortrag.
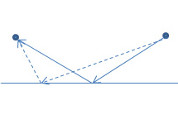
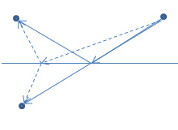
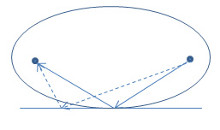
Abb. 2 [links]: Ein Lichtstrahl wird an einer Ebene gespiegelt. Ist die durchgezogene Linie kürzer als die gestrichelte?
Abb. 3 [mitte]: Wenn man den linken Punkt an der Ebene spiegelt, dann ist es auf einen Blick zu sehen, daß die durchgezogene Linie kürzer als die beiden gestrichelten Linien ist.
Abb. 4 [rechts]: Da von jedem Punkt auf der Ellipse die Länge der Summe der Verbindungen zu den beiden Foki immer die gleiche ist und die durchgezogenen Linien auf der Ellipse liegen, die gestrichelten aber außerhalb, ist die Länge der durchgezogenen Linien die kürzest-mögliche Verbindung.
Genie ist erlernbar
Peter Møller eröffnete das Seminar mit einem Vortrag über die physikalische Realität der uns umgebenden Welt. Dazu begann er seinen Vortrag, indem er berichtete, wie Lyndon LaRouche über Wissen nachdachte. Herr LaRouche definierte Wissen als eine neue Hypothese, die der Menschheit mehr Macht über das physikalische Universum gibt als vorhergehende Hypothesen (siehe das obige Beispiel der Dampfmaschine).
Um in der Lage zu sein, neue und bessere Hypothesen bilden zu können, bedarf es viel Übung. Der Vortrag von Peter Møller war eine solche Übung, wozu zunächst einige theoretische Überlegungen über die physikalische Realität angestellt wurden und diese dann in einem einfachen Experiment überprüft wurden.
Die erste Überlegung beschäftigte sich mit der Frage, was die kürzeste Verbindung zwischen zwei Punkten ist, wenn die Entfernung von einem Lichtstrahl zurückgelegt wird, der an einer Ebene gespiegelt wird (siehe Abbildung 2). Die Frage dabei ist, ob die durchgezogene Linie kürzer ist als die gestrichelte, was die nächstliegende Vermutung ist. Ein Teilnehmer hatte die Idee, diese Vermutung mit folgender Argumentation zu begründen: wenn man den linken Punkt an der Ebene spiegelt, dann ist es auf einen Blick zu sehen, daß die eine durchgezogene Linie kürzer als die beiden gestrichelten Linien ist (Abbildung 3).
Eine weitere Begründung wurde vorgebracht, um die Vermutung zu beweisen: wenn man eine Ellipse mit den beiden Punkten als deren Foki einzeichnet und die Ellipse die Ebene, an der sich der Lichtstrahl spiegelt, berühren läßt, dann sieht man leicht, daß die gestrichelten Linien länger als die durchgezogenen Linien sind. Da von jedem Punkt auf der Ellipse die Länge der Summe der Verbindungen zu den beiden Foki immer die gleiche ist und die durchgezogenen Linien auf der Ellipse liegen, die gestrichelten aber außerhalb, ist die Länge der durchgezogenen Linien die kürzest-mögliche Verbindung (Abbildung 4).
Diese erste Überlegung diente vorrangig der Einstimmung und wurde nicht durch ein Experiment ergänzt.
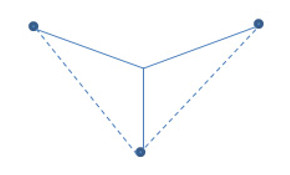 Abb. 5: Was ist die kürzeste Verbindung zwischen drei Punkten: die Summe
der gestrichelten oder die der durchgezogenen Linien?
Abb. 5: Was ist die kürzeste Verbindung zwischen drei Punkten: die Summe
der gestrichelten oder die der durchgezogenen Linien?
Die beiden nächsten Überlegungen wurden durch Experimente überprüft. Dazu wurde zunächst die Frage gestellt, was die kürzeste Verbindung zwischen drei Punkten sei (Abbildung 5): die Summe der gestrichelten oder die der durchgezogenen Linien? Wie die Abbildung zeigt, wurde berechnet, daß es wieder die durchgezogenen Linien sind: nimmt man den einfachsten Fall, daß die drei Punkte ein gleichseitiges Dreieck aufspannen, so ergeben sich (begrenzt durch die durchgezogenen und die gestrichelten Linien) im Inneren dieses gleichseitigen Dreiecks drei gleichschenklige Dreiecke, mit den Schenkellängen zu 2 und der Höhe zu 1, weil die durchgezogenen Linien sich im Schwerpunkt des gleichseitigen Dreiecks treffen und der Schwerpunkt immer die Seitenhalbierenden im Verhältnis 2:1 teilt. Durch eine Überlegung mit Hilfe des Satzes von Pythagoras ergibt sich, daß eine gestrichelte Linie 2x√3 lang sein muß. Somit ist die Summe der durchgezogenen Linien genau 6, die Summe der gestrichelten Linien etwa 6,928. Die gleiche Überlegung wurde mit der kürzesten Verbindung zwischen vier Punkten angestellt und berechnet.
Nun war das Publikum vorbereitet, einen entscheidenden Schritt weiter geführt zu werden: Was ist die kürzeste Verbindung von vier Punkten im Raum, wenn diese durch Flächen verbunden werden?
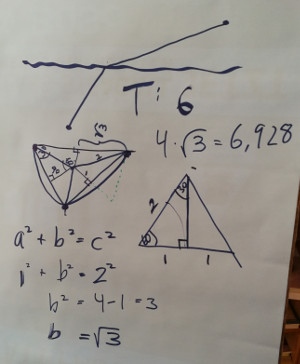
Abb. 6 [rechts]: Die kürzeste Verbindung zwischen vier Punkten im Raum (einem Tetraeder) – gesucht durch geometrische Konstruktionen...
Abb. 7 [unten links]: ... und demonstriert mit Hilfe von Seifenlauge.
Abb. 8 [unten rechts]: Dasselbe Prinzip zeigt sich auch bei der Untersuchung eines Würfels.


Bevor Sie sich das nächste Bild ansehen, stellen Sie sich diese Situation im Kopf vor: Sie haben ein Tetraeder aus Draht vor sich und sind kurz davor, dieses in ein Seifenbad einzutauchen. Was passiert wohl, wenn Sie dieses wieder herausholen? Wie werden sich die vier Flächen anordnen, um die vier Eckpunkte möglichst effizient miteinander zu verbinden? Desgleichen stellen Sie sich vor: was wird wohl passieren, wenn Sie einen Würfel aus Draht aus dem Seifenbad ziehen? Die Abbildungen 6, 7 und 8 geben die Antwort darauf.2
Die Fragen, die sich wiederum daraus ergeben, sind entscheidend und sollten nicht ignoriert werden. Hatten Kues, Leibniz, Bernoulli, Fermat, Brunelleschi u.a. recht und unser Universum verhält sich tatsächlich nach dem sogenannten „Prinzip der kleinsten Wirkung“ (korrekterweise müßte man sagen: Prinzip der größten Wirkung bei kleinstem Aufwand)?
Das soeben durchgeführte Experiment scheint das zu bestätigen. Eine weitere Bestätigung findet sich in der Kuppel der Kathedrale Santa Maria del Fiore in Florenz. Nur dank der genialen Entdeckung Filippo Brunelleschis konnte diese Kuppel überhaupt gebaut werden, denn diese Entdeckung war eine neue Hypothese, die ihm und der Menschheit mehr Macht über das physische Universum gab. Im Sinne LaRouches hatte also Filippo Brunelleschi tatsächlich Wissen geschaffen. Er ließ sich von der Kettenlinie inspirieren und anleiten – eine weitere Ausdrucksform des Prinzips der kleinsten Wirkung. Somit war der Bau möglich, denn die Kuppel trug sich bereits selber, während sie gebaut wurde. Durch Gerüste konnte sie nicht gestützt werden, da in dieser Zeit keine Gerüste dieser Höhe gebaut werden konnten.3
Diese Analogie paßt sehr gut zum Thema unserer Kaderschule: Die menschliche Gesellschaft braucht Menschen, die ohne ein Gerüst die Gesellschaft aus eigener Kraft heraus tragen können! Dazu können Menschen erzogen werden. Dieses ist das Ziel der LaRouche-Bewegung, wie auch in den weiteren Vorträgen ersichtlich wurde.
Musik: die Seele der Gesellschaft
Der anschließende Vortrag befaßte sich mit Musik. Es wurde ein starker Kontrast zwischen der heutigen Musik und klassischer Musik deutlich aufgezeigt, indem der Popsong Shape of you von Ed Sheeran mit Beethovens Liederzyklus An die ferne Geliebte verglichen wurde. Im ersten Lied geht es um die rein körperliche, egoistische Liebe, und zwar unmißverständlich und direkt. Beethovens Komposition verstärkt die Bilder des bereits wunderschönen Gedichttextes (siehe nebenstehenden Kasten) durch ein sehr gelungenes Zusammenspiel von Klavier und Stimme.4
Nachdem der Zuhörer beide Lieder gehört hat, wird der Unterschied des emotionalen Eindrucks, den die beiden Lieder ausüben, sehr deutlich. Leider ist es heutzutage überhaupt nicht mehr Teil unserer Kultur, diese hohen Ideen, die in An die ferne Geliebte zum Ausdruck kommen, zu empfinden, geschweige denn auszudrücken. Diese Form der Liebe ist seelenbezogen. Es geht dem Liebenden um die Schmerzen, die beide empfinden, nicht bloß die eigenen. Außerdem könnte die Geliebte auch jemand sein, den der Liebende noch nie getroffen hat, da diese Form der Liebe allgemein und ideell ist, ähnlich wie die Liebe Dante Alighieris zu Beatrice in der Göttlichen Komödie. Beethovens Lied ist eine Kommunikation der unsterblichen Art, die Raum und Zeit überwindet, was besonders in den letzten beiden Strophen deutlich wird: „Und du singst, was ich gesungen / Was mir aus der vollen Brust / Ohne Kunstgepräng erklungen, / Nur der Sehnsucht sich bewußt: // Dann vor diesen Liedern weichet / Was geschieden uns so weit, /Und ein liebend Herz erreichet / Was ein liebend Herz geweiht.“
 Abb. 9: Erst durch aktive Beteiligung werden Kunst und Musik wirklich
verstehbar.
Abb. 9: Erst durch aktive Beteiligung werden Kunst und Musik wirklich
verstehbar.
Erst wenn der größte Teil der Kultur einer (unserer) Gesellschaft wieder so edel empfinden kann, wird es eine Grundlage geben, eine schöne und moralische Gesellschaft zu errichten, auf dem besten Weg, Brutalität und Kriminalität hinter sich zu lassen.
Zu diesem Zweck hatte der Vortragende ein kurzes Arrangement von An die ferne Geliebte geschrieben, was dann im Chor von allen Teilnehmern gesungen wurde (Abbildung 9).
Am Ende dieses ersten Abends wurde ein kleiner Musikabend mit insgesamt zwölf Darbietungen abgehalten: die Aria aus Bachs Goldberg-Variationen, das Präludium in f-moll (BWV 881), Der Lindenbaum und drei Lieder aus Die schöne Müllerin von Franz Schubert, das Duett „Là ci darem la mano“ aus Mozarts Oper Don Giovanni, Volkslied von Felix Mendelssohn-Bartholdy, Marzellines Arie aus Beethovens Fidelio, Impromptu Nr. 3 von Franz Schubert, „Bei Männern, welche Liebe fühlen“ aus Mozarts Zauberflöte und das Adagio aus Beethovens 1. Klaviersonate.
Die LaRouche-Bewegung hat schon immer viel Wert auf die Bildung des Charakters gelegt, was am besten dadurch geschieht, daß man selber darauf hinarbeitet, entweder eigene, valide Ideen in der Wissenschaft zu entdecken und zu formulieren oder neue, schöne Ideen in der Musik und Kunst zu erschaffen. Beides kann man durch Zwischenschritte erreichen, etwa dadurch, daß man schöne Kompositionen klassischer Musik wahrhaftig präsentiert – und zwar so, daß deren Idee genauso beim Zuhörer ankommt, wie sich der Komponist das gedacht hat.
Der strategische Kontext
Der nächste Tag begann mit dem Vortrag von Harley Schlanger, der gleich zu Beginn die ganz große Frage stellte: Zu welchem Zweck lebt man? Besonders in diesen Zeiten ist das für jeden einzelnen eine wichtige Frage, denn die Menschheit steht potentiell an der Schwelle zu einem Neuen Paradigma; um dieses wirklich zu verwirklichen, kann jeder einen Beitrag leisten, potentiell sogar einen entscheidenden, ohne den die Weltgeschichte ganz anders verlaufen würde.
Um diese Idee zu illustrieren, benutzte Herr Schlanger zwei Beispiele. Zunächst erzählte er von der enormen Bedeutung von Notre Dame de Paris für Frankreich und für die Welt. Seit der Entscheidung im Jahr 1163, diese Kathedrale zu bauen, war sie das Zentrum der Entwicklung Frankreichs. Der damalige Bischof entschied, eine Kathedrale wäre notwendig, um der bereits großen und schnell wachsenden Stadt eine größere Idee zu geben, damit jeder Mensch die Möglichkeit bekam, sich wieder mit seiner eigenen Lebensmission in Einklang zu bringen. Man stelle sich einen hart arbeitenden Bauarbeiter vor, der jeden Tag um sein Überleben kämpft, aber durch diese wunderbare Kathedrale seinen Alltag eine Weile hinter sich lassen, den Blick gen Himmel richten und einen ganz persönlichen Dialog mit seinem Schöpfer führen kann.
Notre Dame de Paris hat die Entwicklung der Stadt von höheren Prinzipien als allein Handel und Profit leiten lassen. Sie ist seit ihrer Idee nicht nur spiritueller Ankerpunkt gewesen, sondern – vor allem während ihres Baus – ein Zentrum der Entwicklung der Baukunst, Glasschmiedekunst, Verarbeitung von Baumaterialien, Holzschnitzerei, Bildhauerei und vielen weiteren Gewerben und Kunstbereichen. Der Bau dieses Gotteshauses war eine riesige wissenschaftliche Herausforderung! Notre Dame verkörpert eine fast tausendjährige Tradition in Paris und Frankreich. Sie ist ein Zeugnis der Unsterblichkeit der individuellen menschlichen Seele sowie der gesamten menschlichen Gattung, was gerade durch das Brandunglück vom 16. April deutlich geworden ist, als annähernd die gesamte Welt um den Verlust trauerte und nun zumindest darin vereint ist, sie wieder aufzubauen.
Das zweite Beispiel der Mission eines jeden Menschen war Schillers Konzept der Universalgeschichte, wie er es ganz explizit in seiner ersten Vorlesung „Was ist und zu welchem Ende studiert man Universalgeschichte?“ dargestellt hat. Schiller schreibt, daß die Menschheitsgeschichte sowohl den Verfall als auch die Veredlung des Menschen zeige, es komme nur darauf an, wofür man sich entscheide – ein echter philosophischer Kopf zu sein, oder ein Brotgelehrter, der vorrangig auf seinen eigenen Vorteil bedacht ist und daher nichts Neues wagt und kein Risiko eingehen wird, um eine Veränderung herbeizuführen.
Von der zweiten Sorte gab es bereits zu Schillers Zeiten mehr als genug, heutzutage gibt es jedenfalls zu viele. Das sind diejenigen, die die Voraussetzungen erfüllen, etwas bewegen zu können (etabliert, gut gebildet, einflußreich), aber vorgeben, daß nur mit genug Unterstützung etwas zu verändern wäre – da dies aber nicht der Fall sei, wäre eine Änderung eben nicht möglich. Das ist, wie Harley Schlanger betonte, ein wesentlicher Zug des oligarchischen Systems! Denn sowohl die Brotgelehrten als auch die Oligarchen lassen keinen Raum für Fortschritt, nur für Unterdrückung. Und so sei es die wesentliche Aufgabe im Leben eines Menschen, die Menschen zu finden, die verzweifeln, und dann herauszufinden, was diese begeistert, um sie zu verändern.
An diesen Vortrag schloß sich eine lebhafte Diskussionsrunde an, in der unter anderem die große Frage gestellt wurde, wie Lyndon LaRouche in der Lage gewesen ist, zutreffende Vorhersagen zu treffen (in seinem Fall vor allem über die Entwicklung der Weltwirtschaft). Denn diese Fähigkeit ist extrem nützlich und notwendig. Man könnte dadurch Katastrophen verhindern, bevor sie eintreten, wie etwa das Feuer von Notre Dame, oder bereits in der Lage sein, Krankheiten zu heilen, bevor sich deren Ursache entwickelt (wie Mutation von Viren und Bakterien).
Harley Schlanger erzählte, er sei nach wie vor zutiefst beeindruckt davon, wie Herr LaRouche bereits am Vorabend der US-Präsidentschaftswahl, bei der G.W. Bush Präsident wurde (im November 2000), sagen konnte, daß man eine ganze Weile nicht wissen werde, wer tatsächlich die Wahlen gewonnen hat. Und tatsächlich dauerte es etwa vier Wochen, und noch nicht einmal dann war es klar, sondern ein Gericht mußte intervenieren und einen Sieger bestimmen. Ihm selbst sei das damals total unbegreiflich gewesen, und auch heute noch sei er sich nicht sicher, wie Herr LaRouche diese Vorhersage treffen konnte. Aber soviel konnte Herr Schlanger dem Publikum sagen: Diese Fähigkeit kann sich potentiell jeder aneignen, es braucht dafür viel Arbeit an sich selbst und an der Realität, wie etwa dem Studium der Geschichte (sowie Wissenschaft).
Kreatives Denken anstatt euklidischer Geometrie
Zuletzt hielt Ilja Karpowski einen Vortrag über sphärische Geometrie, wobei er über das berichtete, was er von dem schottischen Wissenschaftler John Napier (1550-1617) gelernt hat. Anders als in der Ebene sind in der sphärischen Geometrie auch Dreiecke mit mehr oder weniger als 180° möglich; beziehungsweise ist die Kugelgeometrie sogar so gestaltet, daß die Fläche eines jeden Dreiecks bereits definiert ist, sobald man seine Winkel kennt, was wiederum bei der Navigation von Schiffen von großem Vorteil ist.
Der Vortrag begann, indem daran erinnerte wurde, daß Herr LaRouche die euklidische Mathematik immer und vehement abgelehnt hat. Warum? Herr Karpowski nannte einen ersten Hinweis: Ihm fiel auf, daß die euklidischen Definitionen sehr schwammig und nichtssagend seien. „Was keine Teile hat, ist ein Punkt“, heißt es bei Euklid oder: „Eine Linie ist gerade, wenn sie gegen die in ihr befindlichen Punkte auf einerlei Art gelegen ist.“




Herrn LaRouche ging es immer darum, anders über Geometrie nachzudenken und allgemein die eigene Denkmethode zu hinterfragen. Das ist notwendig, um neue Entdeckungen zu machen und nicht in die Fallen der großen Medien zu tappen. Und es ist erlernbar, was das Hauptziel dieser und jeder Kaderschule der LaRouche-Bewegung ist.
Auch hier wandte Herr Karpowski die bewährte Methode an, das Publikum aktiv einzubinden. Es ist ein wesentlicher Fehler des derzeitigen westlichen Bildungssystems, daß zuviel Frontalunterricht betrieben wird, denn nur durch eigene Aktivität lernt man etwas wirklich. Er begann, indem er dem Publikum die relativ einfache Aufgabe stellte, zu beweisen, daß ein ebenes Dreieck tatsächlich und immer eine Innenwinkelsumme von 180° hat. Meine Empfehlung: Versuchen Sie, bevor Sie weiterlesen, diese Frage tatsächlich selbst zu beweisen, es wird sich lohnen!
Als nächstes sollten die Teilnehmer aus Papierstreifen ein Dreieck zusammenstecken, welches drei Winkel von jeweils 90° hat (Abbildung 10). Da alle noch in der Geometrie der Ebene festhingen, war zunächst ein Umdenken notwendig, aber sobald man einfach die drei Streifen zusammengeklebt hatte und darauf achtete, daß jeder Innenwinkel 90° hat, kam als Form ein Achtel einer Kugeloberfläche heraus (siehe Abbildung 11). Im Laufe der Arbeit und Diskussion stellte sich heraus, daß jeder Primzahl ein Polygon auf der Kugel zugeordnet werden kann, bei welchem jeder Winkel 90° groß ist. So etwa ein Fünfeck (siehe Abbildung 12).
Am Ende des Vortrags wies Herr Karpowski auf die unendliche Fülle verschieden geformter nicht-ebener Oberflächen hin, wie etwa hyperbolische Körper, auf deren Oberfläche zum Beispiel Dreiecke mit dreimal 45° möglich sind (siehe Abbildung 13, man beachte die negative Krümmung).
Nun hoffe ich, werter Leser, daß Sie durch diesen Artikel zumindest etwas in den Genuß kommen konnten, die eigene schöpferische Geisteskraft zu bewegen. Genau diese ist es, die uns weit über jede Form der Unterdrückung hinausbegibt:
Der Mensch ist frei geschaffen, ist frei,
Und würd’ er in Ketten geboren,
Laßt euch nicht irren des Pöbels Geschrei,
Nicht den Mißbrauch rasender Toren.
Vor dem Sklaven, wenn er die Kette bricht,
Vor dem freien Menschen erzittert nicht.5
Anmerkungen
1. Siehe Lyndon LaRouche, Was Sie schon immer über Wirtschaft wissen wollten, S. 18.
2. Am besten, Sie führen dieses Experiment selbst zu Hause durch! Es ist eine schier unglaubliche Freude, die uns und unseren Kindern im heutigen Bildungssystem so gut wie immer vorenthalten wird. Für dieses Experiment brauchen Sie nur leicht verbiegbaren Draht und Seifenwasser.
3. Vgl. Karel Vereycken, „Die Geheimnisse des Florentiner Domes lüften“, Neue Solidarität 1-2, 2016.
4. Dieser Liederzyklus kann auf YouTube angehört werden.
5. Aus Friedrich Schiller: „Die Worte des Glaubens“, 1797